해당 자료는 전북대학교 이영미 교수님 2023고급시계열분석 자료임

library(lubridate)
library(ggplot2)
library(car)
#library(forecast)
library(lmtest)


Attaching package: ‘lubridate’


The following objects are masked from ‘package:base’:

    date, intersect, setdiff, union


Loading required package: carData

Loading required package: zoo


Attaching package: ‘zoo’


The following objects are masked from ‘package:base’:

    as.Date, as.Date.numeric

1

z <- c(52,46,46,52,50,50,48,45,41,53)
n <- length(z)

(1)

sum(z)
(bar_z = mean(z))

483

48.3

(3)

sum((z- mean(z))^2)
s2 = sum((z- mean(z))^2)/(n-1)
s2

130.1

14.4555555555556

bar_z + qt(0.975,(n-1)) * sqrt((1+1/n)*s2)
bar_z - qt(0.975,(n-1)) * sqrt((1+1/n)*s2)

57.3206225347423

39.2793774652577

- lm함수 비교

m <- lm(z~1)
summary(m)


Call:
lm(formula = z ~ 1)

Residuals:
   Min     1Q Median     3Q    Max 
  -7.3   -2.3    0.7    3.2    4.7 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)   48.300      1.202   40.17 1.83e-11 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 3.802 on 9 degrees of freedom

predict(m, newdata=data.frame(t=11:15), interval="prediction")

A matrix: 5 × 3 of type dbl
	fit	lwr	upr
1	48.3	39.27938	57.32062
2	48.3	39.27938	57.32062
3	48.3	39.27938	57.32062
4	48.3	39.27938	57.32062
5	48.3	39.27938	57.32062

2

(3)

z <- c(303,298,303,314,303,314,310,324,317,327,323,324,331,330,332)
n <- length(z)

t <- 1:n

hat_beta_0 = 2*(2*n+1)/n/(n-1) * sum(z) - 6/n/(n-1)*sum(t*z)
hat_beta_0
hat_beta_1 = 12/n/(n^2-1)*sum(t*z) - 6/n/(n-1)*sum(z)
hat_beta_1

297.780952380952

2.3857142857143

(4)

$\hat Z_n(l) = \hat \beta_0 + \hat \beta_1(n+l)$

hat_beta_0 + hat_beta_1 *(15+(1:5))

335.952380952381
338.338095238095
340.72380952381
343.109523809524
345.495238095238

- lm비교

m <- lm(z~t)
summary(m)


Call:
lm(formula = z ~ t)

Residuals:
   Min     1Q Median     3Q    Max 
-6.710 -2.331 -1.181  2.519  7.133 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)  297.781      2.364 125.964  < 2e-16 ***
t              2.386      0.260   9.176 4.84e-07 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 4.351 on 13 degrees of freedom
Multiple R-squared:  0.8662,    Adjusted R-squared:  0.856 
F-statistic: 84.19 on 1 and 13 DF,  p-value: 4.836e-07

predict(m, newdata = data.frame(t=15+(1:5)), interval="prediction")

A matrix: 5 × 3 of type dbl
	fit	lwr	upr
1	335.9524	325.2553	346.6495
2	338.3381	327.3932	349.2830
3	340.7238	329.5084	351.9393
4	343.1095	331.6025	354.6166
5	345.4952	333.6771	357.3134

3

note: 모의시계열 표본평균과 표본분산을 안구했었네!;

t <- 1:100
####### (1)
Zt_1 <- 100 + rnorm(100,0,1)
####### (2)
Zt_2 <- 500 + rnorm(100,0,1)
####### (3)
Zt_3 <- 100 + rnorm(100,0,10)
####### (4)
Zt_4 <- 100 + t * rnorm(100,0,1)

dt <- data.frame(
 Zt_1 = Zt_1,
 Zt_2 = Zt_2,
 Zt_3 = Zt_3,
 Zt_4 = Zt_4)
round(colMeans(dt),2)
round(apply(dt,2,var),2)

Zt_1: 100.04
Zt_2: 499.98
Zt_3: 100.45
Zt_4: 95.8

Zt_1: 1.05
Zt_2: 0.84
Zt_3: 89.68
Zt_4: 2449.71

ts.plot(ts(Zt_1), ts(Zt_2), ts(Zt_3), ts(Zt_4),
 lwd=2,
 col= 1:4)
legend(c(0,450), legend = c(expression(Z[t1]), expression(Z[t2]), expression(Z[t3]),expression(Z[t4]),
         col= 1:4, bty='n', lty=1, lwd=2)

ERROR: Error in parse(text = x, srcfile = src): <text>:6:0: unexpected end of input
4: legend(c(0,450), legend = c(expression(Z[t1]), expression(Z[t2]), expression(Z[t3]),expression(Z[t4]),
5:          col= 1:4, bty='n', lty=1, lwd=2)
  ^

4

###### (1)
Zt_1 <- 100 + rnorm(100,0,1)
####### (2)
Zt_2 <- 100 + t + rnorm(100,0,1)
####### (3)
Zt_3 <- 100 + 0.3*t + sin(2*pi*t/12) + cos(2*pi*t/12) + rnorm(100,0,1)

Warning message in 100 + t + rnorm(100, 0, 1):
“longer object length is not a multiple of shorter object length”
Warning message in 100 + 0.3 * t + sin(2 * pi * t/12) + cos(2 * pi * t/12) + rnorm(100, :
“longer object length is not a multiple of shorter object length”

ts.plot(ts(Zt_1), ts(Zt_2), ts(Zt_3),col= 1:3, lwd=2)
legend("topleft", legend = c(expression(Z[t1]), expression(Z[t2]), expression(Z[
 col= 1:3, lty=1, lwd=2)

Zt_1 : 불규칙성분
Zt_2 : 추세성분 + 불규칙 성분
Zt_3 : 추세성분 + 계절성분(주기12) + 불규칙 성분: 계절성분 값이 오차에 비해 너무 작아 확인하기 쉽지 않다.

Zt_3 <- 100 + 0.3*t + 3*sin(2*pi*t/12) + 20*cos(2*pi*t/12) + rnorm(100,0,1)
ts.plot(ts(Zt_1), ts(Zt_2), ts(Zt_3),col= 1:3)
legend("topleft", legend = c(expression(Z[t1]), expression(Z[t2]), expression(Z[
 col= 1:3, lty=1)

5

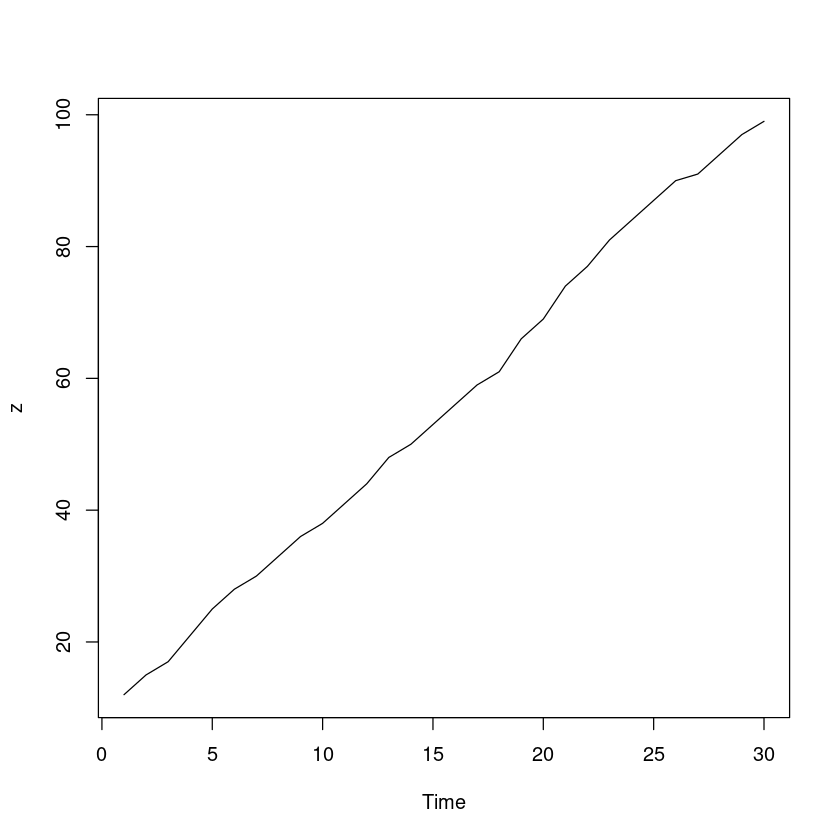
z <- scan("book.txt")
plot.ts(z)

(3)

$Z_t = \beta_0 + \beta_1 t + \epsilon_t$

length(z)

t <- 1:length(z)
m <- lm(z~t)
summary(m)


Call:
lm(formula = z ~ t)

Residuals:
    Min      1Q  Median      3Q     Max 
-2.5563 -1.0063 -0.2081  1.0385  2.0644 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)  8.19080    0.46960   17.44   <2e-16 ***
t            3.07586    0.02645  116.28   <2e-16 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 1.254 on 28 degrees of freedom
Multiple R-squared:  0.9979,    Adjusted R-squared:  0.9979 
F-statistic: 1.352e+04 on 1 and 28 DF,  p-value: < 2.2e-16

(4)

$\hat Z_{n+l} = \hat Z_n(l) = \hat \beta_0 + \hat \beta_1(n+l)$

new_dt <- data.frame(t=30+(1:12))
predict(m, new_dt)

1: 103.542528735632
2: 106.618390804598
3: 109.694252873563
4: 112.770114942529
5: 115.845977011494
6: 118.92183908046
7: 121.997701149425
8: 125.073563218391
9: 128.149425287356
10: 131.225287356322
11: 134.301149425287
12: 137.377011494253

pred <- predict(m, new_dt, interval="prediction")
pred

A matrix: 12 × 3 of type dbl
	fit	lwr	upr
1	103.5425	100.7996	106.2855
2	106.6184	103.8584	109.3784
3	109.6943	106.9162	112.4723
4	112.7701	109.9731	115.5671
5	115.8460	113.0291	118.6629
6	118.9218	116.0842	121.7595
7	121.9977	119.1384	124.8570
8	125.0736	122.1918	127.9554
9	128.1494	125.2443	131.0546
10	131.2253	128.2960	134.1546
11	134.3011	131.3469	137.2554
12	137.3770	134.3970	140.3570

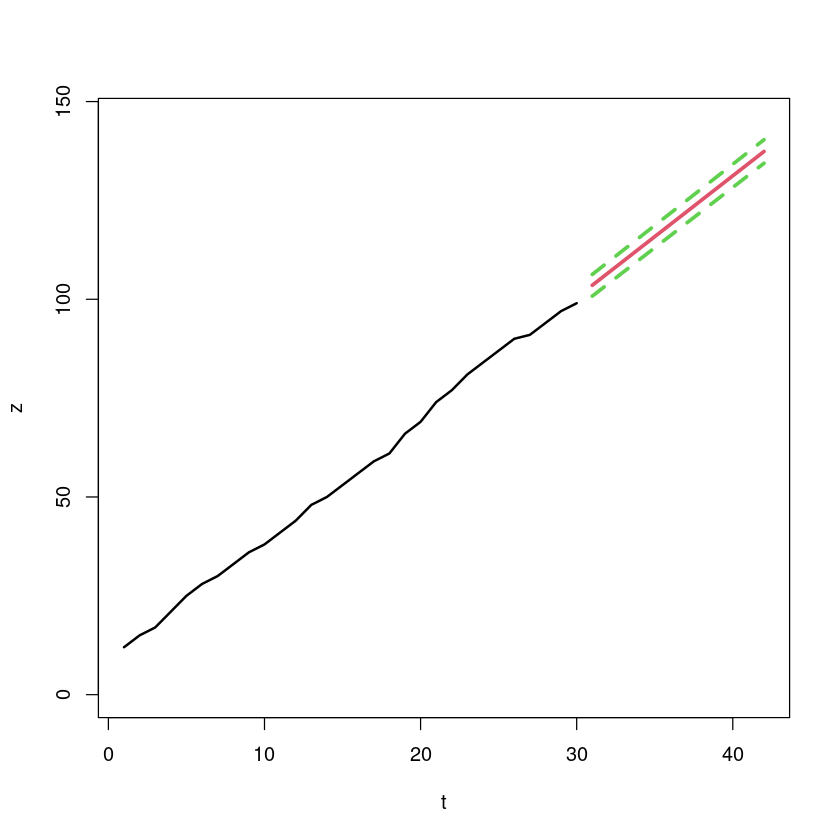
plot(t, z, type='n', ylim = c(0, 145), xlim=c(1,(30+12)))
lines(t, z, lwd=2)
lines(30+(1:12), pred[,1], col=2, lwd=3)
lines(30+(1:12), pred[,2], col=3, lwd=3, lty=2)
lines(30+(1:12), pred[,3], col=3, lwd=3, lty=2)

6

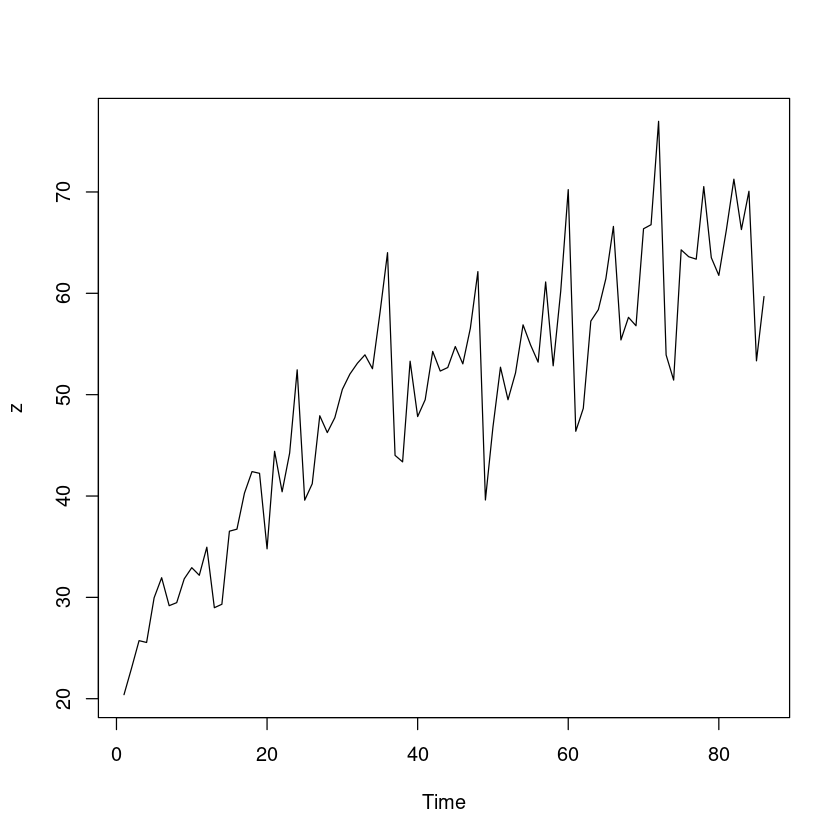
z <- scan("export.txt")
n <- length(z)
n

z_ts <- ts(z, frequency=12)
cycle(z_ts)

A Time Series: 8 × 12
	Jan	Feb	Mar	Apr	May	Jun	Jul	Aug	Sep	Oct	Nov	Dec
1	1	2	3	4	5	6	7	8	9	10	11	12
2	1	2	3	4	5	6	7	8	9	10	11	12
3	1	2	3	4	5	6	7	8	9	10	11	12
4	1	2	3	4	5	6	7	8	9	10	11	12
5	1	2	3	4	5	6	7	8	9	10	11	12
6	1	2	3	4	5	6	7	8	9	10	11	12
7	1	2	3	4	5	6	7	8	9	10	11	12
8	1	2

plot.ts(z)

plot.ts(log(z))

추세성분, 계절성분(주기=12), 불규칙 성분으로 구성되어 있음

계절추세모형

$Z_t = \beta_0+ \beta_1t + \sum_{i=1}^12 \delta_i \times I_{t1} + \epsilon_t$, 단 $\delta_1=0$

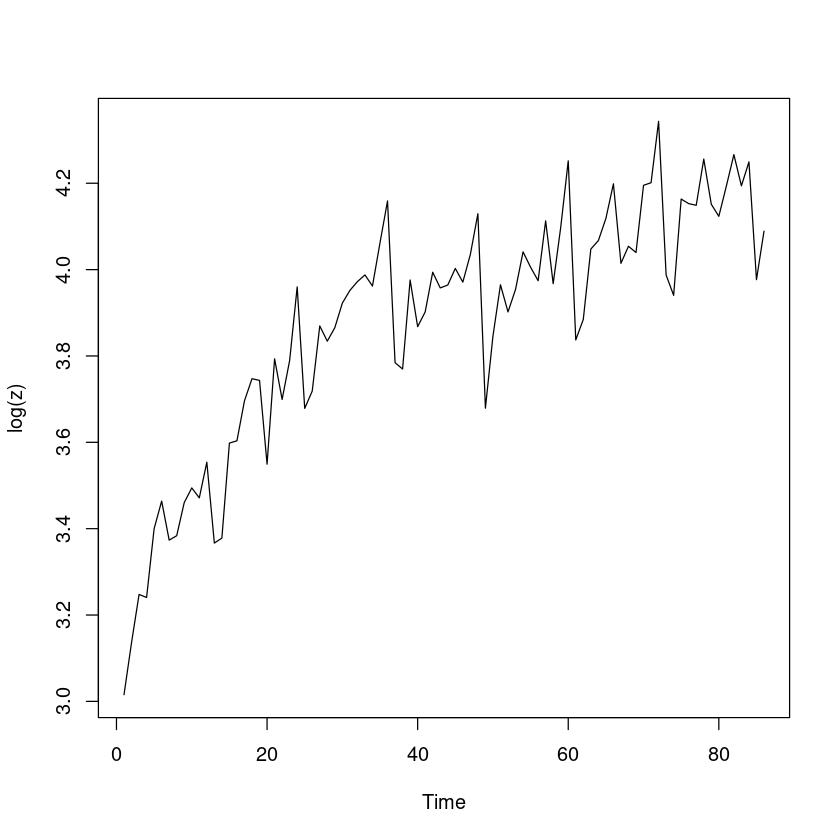
note: 나는 로그변환 한 값을 넣었음

z_ts <- ts(z, frequency=12)
cycle(z_ts)

A Time Series: 8 × 12
	Jan	Feb	Mar	Apr	May	Jun	Jul	Aug	Sep	Oct	Nov	Dec
1	1	2	3	4	5	6	7	8	9	10	11	12
2	1	2	3	4	5	6	7	8	9	10	11	12
3	1	2	3	4	5	6	7	8	9	10	11	12
4	1	2	3	4	5	6	7	8	9	10	11	12
5	1	2	3	4	5	6	7	8	9	10	11	12
6	1	2	3	4	5	6	7	8	9	10	11	12
7	1	2	3	4	5	6	7	8	9	10	11	12
8	1	2

seasonal_I <- as.factor(cycle(z_ts))
t <- 1:n
m2 <- lm(z~t+seasonal_I)

summary(m2)


Call:
lm(formula = z ~ t + seasonal_I)

Residuals:
     Min       1Q   Median       3Q      Max 
-10.8562  -2.2938   0.1567   2.6730   9.3951 

Coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept)  21.98000    1.73500  12.669  < 2e-16 ***
t             0.43721    0.01893  23.097  < 2e-16 ***
seasonal_I2   1.71779    2.16697   0.793 0.430512    
seasonal_I3   9.21741    2.24422   4.107 0.000103 ***
seasonal_I4   7.37163    2.24366   3.286 0.001566 ** 
seasonal_I5   9.30299    2.24326   4.147 8.98e-05 ***
seasonal_I6  12.96578    2.24302   5.780 1.72e-07 ***
seasonal_I7   9.16286    2.24294   4.085 0.000112 ***
seasonal_I8   7.73422    2.24302   3.448 0.000941 ***
seasonal_I9  11.07272    2.24326   4.936 4.88e-06 ***
seasonal_I10 10.68409    2.24366   4.762 9.47e-06 ***
seasonal_I11 12.37545    2.24422   5.514 5.03e-07 ***
seasonal_I12 18.57967    2.24494   8.276 4.26e-12 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 4.334 on 73 degrees of freedom
Multiple R-squared:  0.9011,    Adjusted R-squared:  0.8848 
F-statistic:  55.4 on 12 and 73 DF,  p-value: < 2.2e-16

적합된 모형: $\hat Z_t = 21.98 + 0.437t + 1.72 I_{t2} + 9.22 I_{t3} + \dots 18.58 I_{t12}$

(4) 모형설명(제약조건 주의!)

1개월이 지날 때마다 월별수출액은 평균적으로 0.437억$증가
2월은 1월에 비해 월별수출액이 1.72억$ 증가
3월은 1월에 비해 월별수출액이 9.22억$ 증가
…
12월은 1월에 비해 평균 월별수출액이 18.58억$ 증가

(5)

$\hat Z_{n+l} = \hat Z_n(l) = \hat \beta_0 + \hat \beta_1(n+l) + \sum_{i=1}^{12} \delta_i I_{t1}$

new_dt <- data.frame( t = n + (1:12),
 seasonal_I = as.factor(c(3:12,1,2)))
new_dt

A data.frame: 12 × 2
t	seasonal_I
<int>	<fct>
87	3
88	4
89	5
90	6
91	7
92	8
93	9
94	10
95	11
96	12
97	1
98	2

(6) 95% 예측 구간

predict(m2, new_dt)

1: 69.2346153846154
2: 67.8260439560439
3: 70.1946153846154
4: 74.2946153846154
5: 70.9289010989011
6: 69.9374725274725
7: 73.7131868131868
8: 73.7617582417582
9: 75.8903296703297
10: 82.5317582417582
11: 64.3892994505495
12: 66.5442994505494

pred <- predict(m2, new_dt, interval = 'prediction')
pred

A matrix: 12 × 3 of type dbl
	fit	lwr	upr
1	69.23462	59.82517	78.64407
2	67.82604	58.41659	77.23549
3	70.19462	60.78517	79.60407
4	74.29462	64.88517	83.70407
5	70.92890	61.51945	80.33835
6	69.93747	60.52802	79.34692
7	73.71319	64.30374	83.12264
8	73.76176	64.35231	83.17121
9	75.89033	66.48088	85.29978
10	82.53176	73.12231	91.94121
11	64.38930	55.00439	73.77421
12	66.54430	57.15939	75.92921

69.23462 = $\hat Z_{87} = \hat Z_{86}(1) = \hat \beta_0 + \hat \beta_1 \times 87 + \delta_3 \times I_{87 \times 3}$ (3월)

70.92890 = $ Z_{86}(5) = _0 + _1 (86+5) + 7 I{91 }$ (7월)

(7)

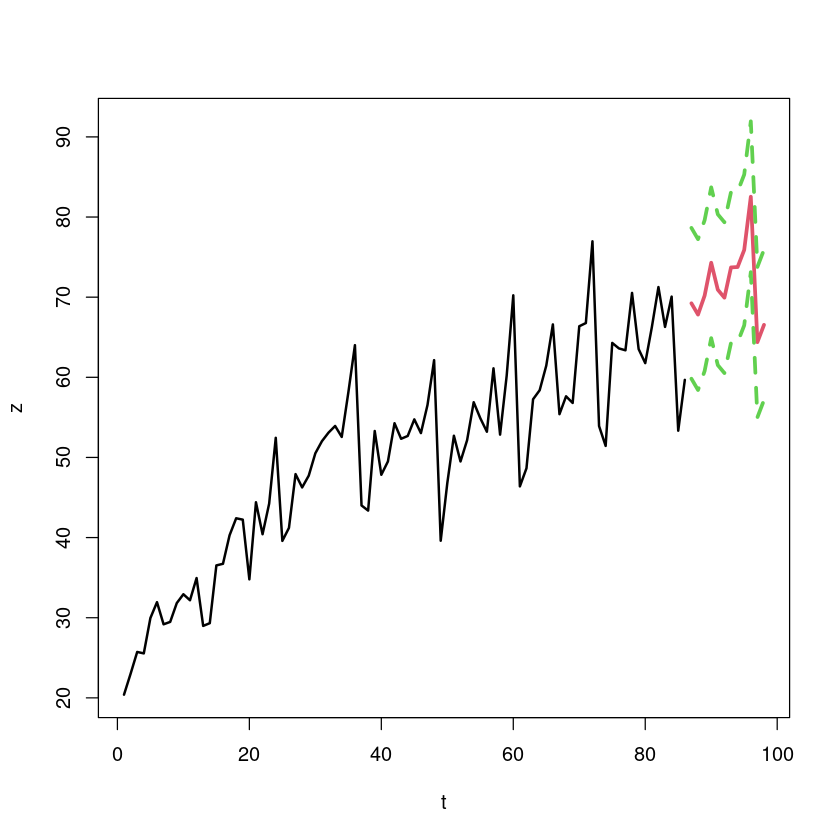
min_ <- min(c(z, pred[,2]))
max_ <- max(c(z, pred[,3]))
plot(t, z, type='n', ylim = c(min_, max_), xlim=c(1,(n+12)))
lines(t, z, lwd=2)
lines(n+(1:12), pred[,1], col=2, lwd=3)
lines(n+(1:12), pred[,2], col=3, lwd=3, lty=2)
lines(n+(1:12), pred[,3], col=3, lwd=3, lty=2)

(번외) 잔차검정

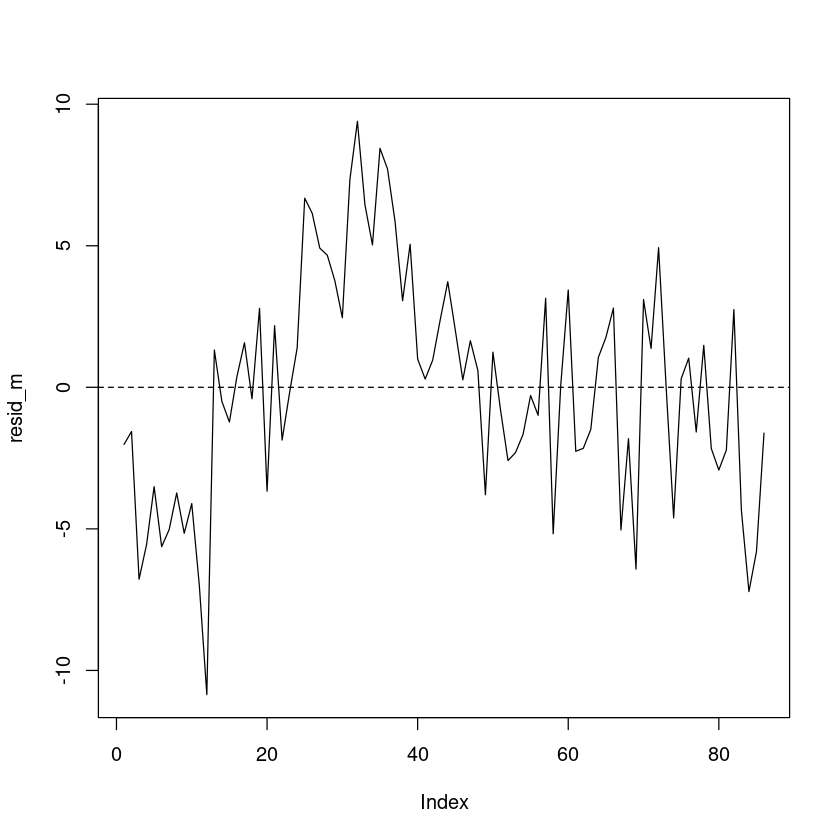
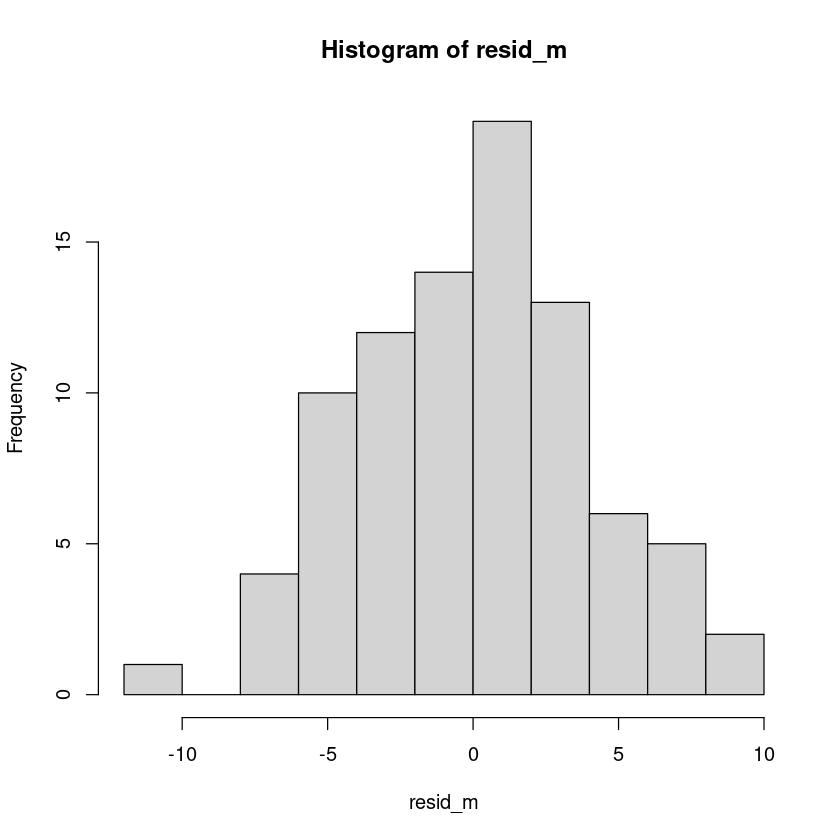
resid_m <- resid(m2)
plot(resid_m, pch=16, type='l')
abline(h=0, lty=2)

t.test(resid_m)


    One Sample t-test

data:  resid_m
t = 2.6111e-16, df = 85, p-value = 1
alternative hypothesis: true mean is not equal to 0
95 percent confidence interval:
 -0.861081  0.861081
sample estimates:
   mean of x 
1.130835e-16

hist(resid_m)

lmtest::bptest(m2)


    studentized Breusch-Pagan test

data:  m2
BP = 18.466, df = 12, p-value = 0.1023

lmtest::dwtest(m2, alternative="two.sided")


    Durbin-Watson test

data:  m2
DW = 0.79196, p-value = 5.014e-09
alternative hypothesis: true autocorrelation is not 0

다항추세 사용

m3 <- lm(z ~ t + I(t^2) + seasonal_I)
summary(m3)


Call:
lm(formula = z ~ t + I(t^2) + seasonal_I)

Residuals:
    Min      1Q  Median      3Q     Max 
-9.2252 -2.1156  0.0414  2.2895  7.5664 

Coefficients:
               Estimate Std. Error t value Pr(>|t|)    
(Intercept)  17.3011107  1.6527443  10.468 4.12e-16 ***
t             0.7955399  0.0637685  12.475  < 2e-16 ***
I(t^2)       -0.0041187  0.0007103  -5.799 1.65e-07 ***
seasonal_I2   1.7177908  1.8014987   0.954 0.343510    
seasonal_I3   8.5584096  1.8691776   4.579 1.91e-05 ***
seasonal_I4   6.6796790  1.8690680   3.574 0.000633 ***
seasonal_I5   8.5863287  1.8690137   4.594 1.81e-05 ***
seasonal_I6  12.2326445  1.8690050   6.545 7.54e-09 ***
seasonal_I7   8.4214835  1.8690354   4.506 2.50e-05 ***
seasonal_I8   6.9928457  1.8691016   3.741 0.000365 ***
seasonal_I9  10.3395882  1.8692037   5.532 4.84e-07 ***
seasonal_I10  9.9674253  1.8693449   5.332 1.07e-06 ***
seasonal_I11 11.6835000  1.8695317   6.249 2.59e-08 ***
seasonal_I12 17.9206692  1.8697737   9.584 1.72e-14 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 3.603 on 72 degrees of freedom
Multiple R-squared:  0.9326,    Adjusted R-squared:  0.9204 
F-statistic: 76.58 on 13 and 72 DF,  p-value: < 2.2e-16

summary(m2)


Call:
lm(formula = z ~ t + seasonal_I)

Residuals:
     Min       1Q   Median       3Q      Max 
-10.8562  -2.2938   0.1567   2.6730   9.3951 

Coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept)  21.98000    1.73500  12.669  < 2e-16 ***
t             0.43721    0.01893  23.097  < 2e-16 ***
seasonal_I2   1.71779    2.16697   0.793 0.430512    
seasonal_I3   9.21741    2.24422   4.107 0.000103 ***
seasonal_I4   7.37163    2.24366   3.286 0.001566 ** 
seasonal_I5   9.30299    2.24326   4.147 8.98e-05 ***
seasonal_I6  12.96578    2.24302   5.780 1.72e-07 ***
seasonal_I7   9.16286    2.24294   4.085 0.000112 ***
seasonal_I8   7.73422    2.24302   3.448 0.000941 ***
seasonal_I9  11.07272    2.24326   4.936 4.88e-06 ***
seasonal_I10 10.68409    2.24366   4.762 9.47e-06 ***
seasonal_I11 12.37545    2.24422   5.514 5.03e-07 ***
seasonal_I12 18.57967    2.24494   8.276 4.26e-12 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 4.334 on 73 degrees of freedom
Multiple R-squared:  0.9011,    Adjusted R-squared:  0.8848 
F-statistic:  55.4 on 12 and 73 DF,  p-value: < 2.2e-16

2차 추세도 유의하고, 수정된 결정계수의 값이 증가 하였기 때문에 2차 추세 모형 사용 가능

resid_m3 <- resid(m3)

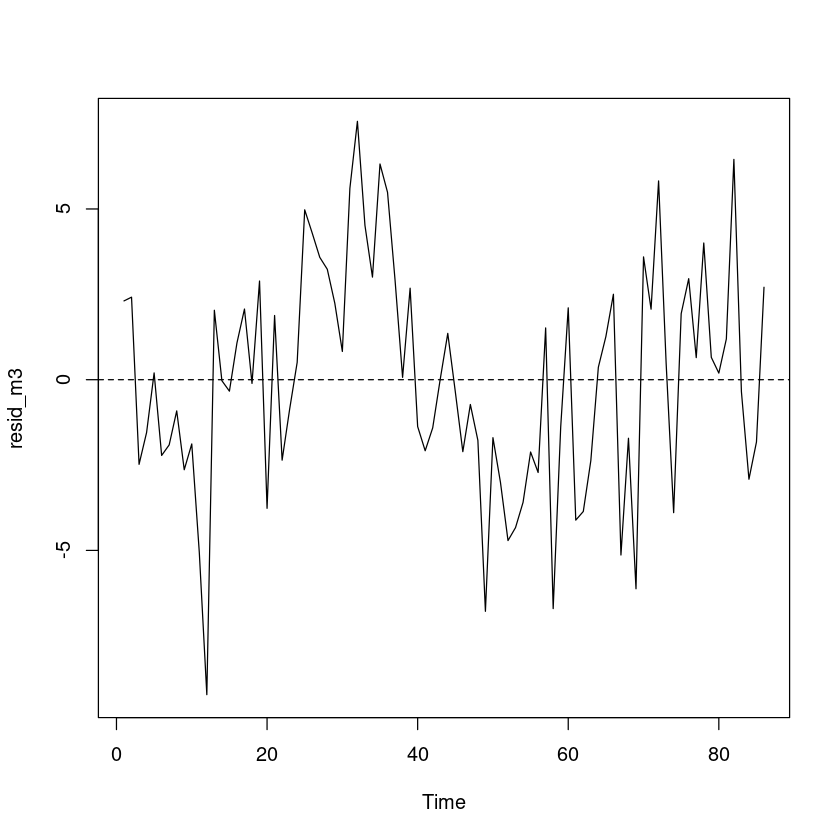
plot.ts(resid_m3)
abline(h=0, lty=2)

t.test(resid_m3)


    One Sample t-test

data:  resid_m3
t = -4.2693e-16, df = 85, p-value = 1
alternative hypothesis: true mean is not equal to 0
95 percent confidence interval:
 -0.7109349  0.7109349
sample estimates:
    mean of x 
-1.526557e-16

lmtest::bptest(m3)


    studentized Breusch-Pagan test

data:  m3
BP = 11.389, df = 13, p-value = 0.5783

lmtest::dwtest(m3)


    Durbin-Watson test

data:  m3
DW = 1.1633, p-value = 4.187e-05
alternative hypothesis: true autocorrelation is greater than 0